音とは？～物理的な側面からの考察～

演者として音楽に携わっている方の多くは、歌声や楽器で良い音、自分が出したいとイメージしている音をどうすれば出せるのか？について、常日頃考えておられるのではないかと思います。

そのためには、日々の鍛錬が必要なことは言うまでもないのですが、音を物理的な側面から理解することも、そこにたどり着くための指針を得ことに繋がると、ウン十年、工学系の研究開発畑で生き抜いてきたバリバリの理系人間であるMASAは考えております。

そこで、本日は物理的な側面からの『音』についてお話ししてみようと思います。

理系ではない方々でも理解しやすいようになるべく平易な説明を心掛けていますが、わかりにくかったらごめんなさい。

音の原理

音は空気振動という物理現象であり、その空気振動（気圧変化）が人の鼓膜に届き振動させることにより、音として認知されます。

振動は、物体の周りにある空気を押し出し、押し出された空気は圧縮されて空気の濃い部分ができます。すると、隣の空気をさらに押し出します。
このように順々に空気の濃い部分と薄い部分（空気の圧力変化）が発生し、それが波となって伝わって行きます（図1）。
この圧力変化の波を「音波」といい、音の密度を表したものを波の形で表したものが正弦波（図2）です。¹⁾

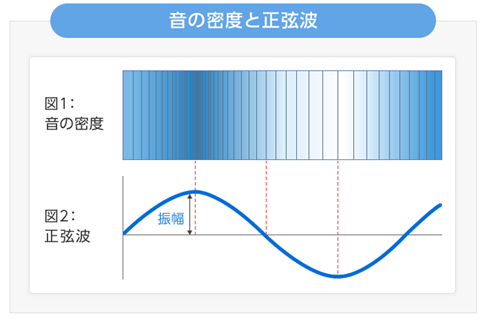
図1　音の密度＆図2　正弦波¹⁾

音の大きさ（強さ）

音の大きさ（強さ）は、空気の圧力の変化量によって決まり、以下の図3に示したように圧力の大きさ（正弦波の振幅）が大きいほど、大きな音となります。¹⁾

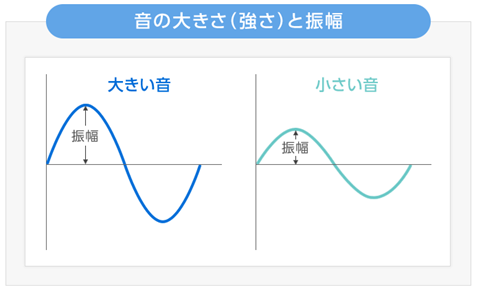
図3　音の大きさ（強さ）と振幅¹⁾

音の高さ

音の高さは1秒間に空気が振動する回数（周波数）で決まり、以下の図4で示した通り回数が多ければ高い音、少なければ低い音となります¹⁾

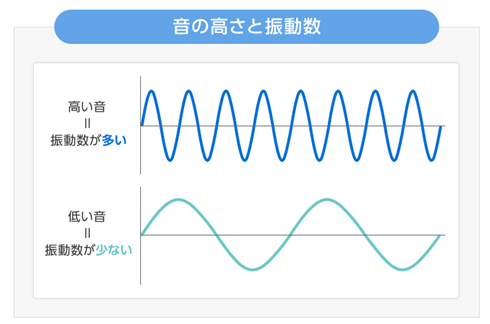
図4　音の高さと振動数¹⁾

音色

同じ大きさや、同じ高さの音を聴いても、ピアノとバイオリンの音は明らかに異なりますよね。これは「倍音」の含まれ方が楽器によって変わるからです。

倍音とは、基音（基準の音）の整数倍の周波数を持つ音で、基音に倍音が重なることで「音色」が構成されます。
倍音が多くなると明るい音に、少ないと暗い音となって聞こえます。¹⁾

倍音の具体例

基音のn倍の周波数を持つ倍音を、第n倍音と呼び、それを低い方から順に並べたものを倍音列と呼びます。基音をC(ド)にした時の倍音列は図5のようになります。

図5　基音をC2にした時の倍音列

ちなみに、1つの周波数の正弦波のみの音（倍音が含まれていない音）を純音と言います。

音は倍音の集合体

『周期的な波は、周波数が整数倍の正弦波を足し合わせて作ることができる。』

これは、フランスの数学者・物理学者ジョゼフ・フーリエが提唱したフーリエの法則です。

すなわち、どんな音も基音とその倍音の組み合わせでできているということです。

ちなみに、理系の大学生ならば、数学の講義で『フーリエ級数』とか『フーリエ展開』とかを学んだこと、少なくとも名称だけでも憶えておられる方が多いと思います。
これは、フーリエの法則を基にした、『複雑な波形を単純な波形（正弦波）に分解する数学的手法』のことで、音（音響学）以外にも電子工学や量子力学、振動工学等々、様々な分野で使われている手法になります。